最简单的图优化G2O使用详解
栏目:行业资讯 发布时间:2024-09-09
图优化理论现在是SLAM领域的主流优化方式,原理知识很多,这里不能一一介绍记录。简单的梳理以下什么是G2O。个人理解,图优化把优化问题考虑成图的模式。带优化的变量称为顶点,对于待优量的限制条件,设定为边的概念,就构成了我们理解
图优化理论现在是SLAM领域的主流优化方式,原理知识很多,这里不能一一介绍记录。简单的梳理以下什么是G2O。
个人理解,图优化把优化问题考虑成图的模式。带优化的变量称为顶点,对于待优量的限制条件,设定为边的概念,就构成了我们理解上的图。
在这里我们把限制条件理解成损失函数,这个函数是优化的关键,我们要通过不断的迭代获取最小的损失,而这又引出了最小二乘法的概念。
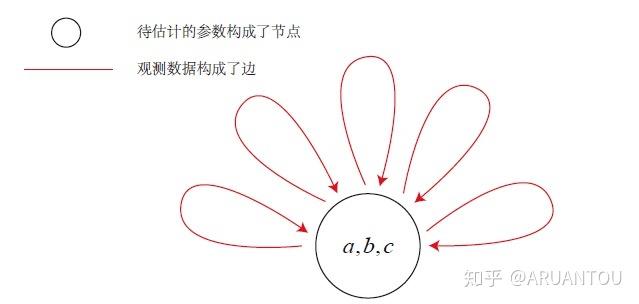
上图就是一个单元图,只有一个优化顶点,通过迭代所有边,求最小二乘。
具体的g2o概念后续会在SLAM的优化中一点点记录。
我们现在看看最简单的应用g2o实现优化求解的方法。
我们来拟合优化一个二次方程:
如果想要拟合这个二次方程,必须求出系数(1,2,1)。这个三位向量就是我们所需要的顶点,那么限制又是什么呢?就是观测值和实际值的差,我们可以用一个最小二乘来表示:
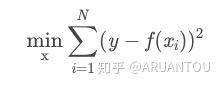
我们先来构造出我们需要的观测数据,x 和 f(x)。我们在这里增加了误差,来表示现实世界中的情况。
// 真实参数,假设曲线是f(x)=a*x^2+b*x+c,真实情况下应该是f(x)=x^2+2*x+1
double a = 1.0,b=2.0,c =1.0;
int N = 100;// 数据点的数量
double w_sigma = 1.0;// 噪声的方差Sigma
//cv::RNG rng;// opencv随机数产生器,如果要使用opencv的高斯0均值随机数发生器,请在commonBased引入[将注释取消即可]
double abc[3] = {0,0,0};// abc参数的估计值
std::vector<double> x_data,y_data;//保存随机数的值,即模拟真实点的情况
std::cout << "\ \ \ \ generating data:" << std::endl;
std::cout << "====================================================" << std::endl;
for(auto i=0;i<N;i++)
{
double x = i/100.0;
x_data.push_back(x);
y_data.push_back(
//exp(a*x*x+b*x+c)+rng.gaussian(w_sigma)
exp(a*pow(x,2)+b*x+c)+g2o::Sampler::gaussRand(0,w_sigma)// 采用G2O的随机发生器
);
std::cout << x_data[i] << " " << y_data[i] << std::endl;
}
接下来就是创建边和顶点。
顶点头文件:
class curveVetex: public g2o::BaseVertex<3,Eigen::Vector3d>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
virtual void setToOriginImpl();
virtual void oplusImpl(const double* update);
virtual bool read(std::istream &is);
virtual bool write(std::ostream &os) const;
};源文件:
void curveVetex::setToOriginImpl()
{
_estimate << 0,0,0;
}
void curveVetex::oplusImpl(const double* update)
{
_estimate +=Eigen::Vector3d(update);
}
bool curveVetex::read(std::istream &is)
{
is >> _estimate[0]>> _estimate[1]>> _estimate[2];
return true;
}
bool curveVetex::write(std::ostream &os) const
{
os << _estimate[0]<< _estimate[1]<< _estimate[2];
return os.good();
}边的头文件:
class curveEdge : public g2o::BaseUnaryEdge<1,double,curveVetex>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
curveEdge (double x):g2o::BaseUnaryEdge<1,double,curveVetex>(),_x (x){}
// 计算曲线模型误差
void computeError();
//存取
bool read(std::istream& is);
bool write(std::ostream& os) const;
public:
double _x;//x值,y值为_measurement
};源文件:
void curveEdge::computeError()
{
// 一元超边,超边存储的节点为VertexContainer类型,你可以把它当成一个数组,取第一个就是0,对于一元边来说,这就是它的
// 连接的边
const curveVetex *v=static_cast<const curveVetex*>(_vertices[0]);
const Eigen::Vector3d abc=v->estimate();
// _error是传入时定义的误差ErrorVector,维度D是构建curveEdge已经定义,必然是个向量,只不过是Eigen::Matrix的_Cols为1
_error(0,0)=_measurement-std::exp(abc[0]*pow(_x,2)+abc[1]*_x+abc[2]);// y-f(x)=error
}
bool curveEdge::read(std::istream &is)
{
is >> _x;
return true;
}
bool curveEdge::write(std::ostream &os) const
{
os << _x;
return os.good();
}代码已经添加了注释,注意看
最后对100个数据进行迭代求最小二乘损失函数。看下整体的代码,包括添加顶点和边到图中后执行优化。
#include <iostream>
#include <g2o/stuff/sampler.h>
#include <g2o/core/block_solver.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <g2o/core/optimization_algorithm_levenberg.h>
#include <g2o/core/sparse_optimizer.h>
#include <chrono>
#include "curveVetex.h"
#include "curveEdge.h"
using namespace std;
int main(int argc,char **argv)
{
std::cout << "====================================================" << std::endl;
std::cout << "\ \ \ \ 这是关于曲线拟合的例子" << std::endl;
std::cout << "====================================================" << std::endl;
std::cout << "\ \ \ \ anthor:YikaiMao" << std::endl;
std::cout << "====================================================" << std::endl;
std::cout << "\ \ \ \ reference:gaoxiang" << std::endl;
std::cout << "====================================================" << std::endl;
// 真实参数,假设曲线是f(x)=a*x^2+b*x+c,真实情况下应该是f(x)=x^2+2*x+1
double a=1.0,b=2.0,c=1.0;
int N=100;// 数据点的数量
double w_sigma=1.0;// 噪声的方差Sigma
//cv::RNG rng;// opencv随机数产生器,如果要使用opencv的高斯0均值随机数发生器,请在commonBased引入[将注释取消即可]
double abc[3]={0,0,0};// abc参数的估计值
std::vector<double> x_data,y_data;//保存随机数的值,即模拟真实点的情况
std::cout << "\ \ \ \ generating data:" << std::endl;
std::cout << "====================================================" << std::endl;
for(auto i=0;i<N;i++)
{
double x=i/100.0;
x_data.push_back(x);
y_data.push_back(
//exp(a*x*x+b*x+c)+rng.gaussian(w_sigma)
exp(a*pow(x,2)+b*x+c)+g2o::Sampler::gaussRand(0,w_sigma)// 采用G2O的随机发生器
);
std::cout << x_data[i]<< " " << y_data[i]<< std::endl;
}
std::cout << "====================================================" << std::endl;
std::cout << "\ \ \ \ 构建图:" << std::endl;
//H矩阵块
using BlockSolverType=g2o::BlockSolverPL<3, 1>;
using LinearSolverType=g2o::LinearSolverDense<BlockSolverType::PoseMatrixType>;
//LM算法
auto solver=new g2o::OptimizationAlgorithmLevenberg(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm(solver);// 设置求解器
optimizer.setVerbose(true);// 打开调试输出
curveVetex* v=new curveVetex();
v->setEstimate(Eigen::Vector3d(0,0,0));
v->setId(0);
optimizer.addVertex(v);
for(int i=0 ; i < N; i++)
{
curveEdge* edge=new curveEdge(x_data[i]);
edge->setId(i);// 边的编号
edge->setVertex(0,v);//设置超边的第几个顶点是什么顶点,目前只有一个顶点
edge->setMeasurement(y_data[i]);//设置观测值
edge->setInformation(Eigen::Matrix<double ,1,1>::Identity()/**1/(w_sigma*w_sigma)*/);//信息矩阵是协方差的逆,1/sigma^2
optimizer.addEdge(edge);// 图中加入顶点
}
std::cout << "\ \ \ \ 构建完成" << std::endl;
std::cout << "====================================================" << std::endl;
std::cout << "\ \ \ \ start optimization" << std::endl;
std::chrono::steady_clock::time_point t1=std::chrono::steady_clock::now();
optimizer.initializeOptimization();
optimizer.optimize(100);
std::chrono::steady_clock::time_point t2=std::chrono::steady_clock::now();
std::chrono::duration<double> time_used=std::chrono::duration_cast<std::chrono::duration<double>> (t2-t1);
std::cout << "====================================================" << std::endl;
std::cout << "\ \ solve time cost="<< time_used.count() << "seconds" <<std::endl;
std::cout << "====================================================" << std::endl;
Eigen::Vector3d abc_estimate=v->estimate();
std::cout << "\ \ estimated model:" << abc_estimate.transpose() << std::endl;
return 0;
}结果如下:
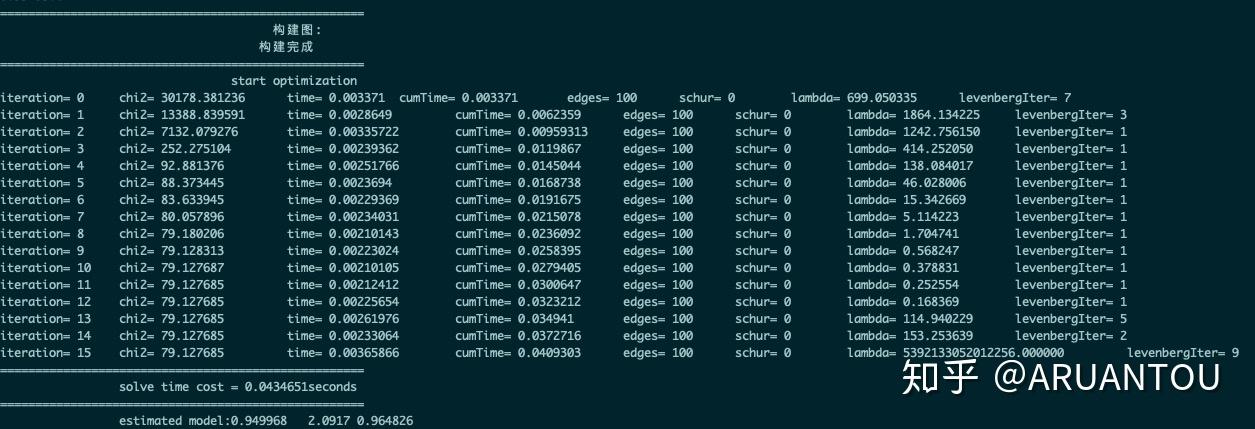
可以看到最后的结果接近(1,2,1)。



